JEE 2013 :: Advanced 2013 :: Mathematics 2013

• Advanced 2013 - Physics 2013
• Advanced 2013 - Chemistry 2013
• Advanced 2013 - Mathematics 2013

 The number of points in (-$\infty$, $\infty$) . for  which   $x^{2}-x\sin x-\cos x=0$ is

Answer:

Explanation:

Concept involved

 The given equation contains algebraic  and trigonometric function called transcendal equation . To solve transcendal  equations we should  always plot the graph for LHS  and RHS

Here,   $x^{2}=x\sin x+\cos x$

Let f(x)= x²  and   g(x) = x sin x+cos x

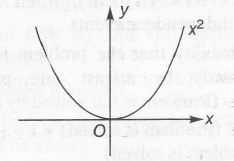
 we know the graph for f(x)= x²

 To plot , g(x) = x sinx+cos x

 g'(x) = x cos x+sinx-sinx 

            g'(x)= x cos x   .....(i)

 g"(x) =- x sinx +cos x  ......(ii)

 put  g'(x)=0

    $\Rightarrow $    x cos x=0

 $\therefore$         $x=0,\frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2},\frac{7\pi}{2},....$

at x=0,  $\frac{3\pi}{2},\frac{7\pi}{2}$,....f"(x) >0

 $\therefore$ minimum

   at x= $\frac{\pi}{2},\frac{5\pi}{2},\frac{9\pi}{2}$,.... f"(x)<0

minimum

  $\therefore$    f(x) and g(x) are shown as

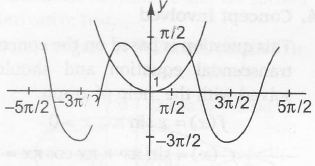
 $\therefore$   Number of solutions are 2.

let   $f:[\frac{1}{2},1]\rightarrow R$ ( the set of all real numbers) be a positive, non -constant and differentiable function such that f'(x)<2f(x)  and   $f(\frac{1}{2})=1$   .Then , the value of   $\int_{1/2}^{1} f(x) dx$ lies in the interval 

Answer:

Explanation:

Concept involved 

 When evere we have linear differential equation containing inequality we should always check for increasing or decreasing 

i.e, for    $\frac{dy}{dx}+Py<0$

   $\Rightarrow$     $\frac{dy}{dx}+Py>0$

 Multiply by integrating factor i.e, $e^{\int_{}^{}Pdx }$  and  convert into total differential equation

 Here, f'(x) <2 f(x) , multiplying by  $e^{-\int_{}^{}2dx }$

 $f'(x).e^{-2x}-2e^{-2x}f(x)<0$

 $\Rightarrow$     $  \frac{d}{dx} (f(x).e^{-2x}) <0$

$\therefore$     $\phi(x)=f(x)e^{-2x}$   is decreasing for   $x \in \left[\frac{1}{2},1\right]$

 thus, when  x >1/2

       $\phi(x) < \phi(\frac{1}{2})$

$\Rightarrow$      $ e^{-2x} f(x)<e^{-1}.f(\frac{1}{2})$

 $\Rightarrow$      $ f(x)<e^{2x-1}.1 given f(\frac{1}{2})=1$

$\Rightarrow$      $0< \int_{1/2}^{1} f(x) dx <\int_{1/2}^{1} e^{2x-1}dx$

$\Rightarrow$     $0< \int_{1/2}^{1} f(x) dx <\left(\frac{e^{2x-1}}{2}\right)^{1}_{1/2}$

$\Rightarrow$        $0< \int_{1/2}^{1} f(x) dx <\frac{e-1}{2}$

A curve passes through the point   $(1,\frac{\pi}{6})$ let the slope of the curve at each point  (x,y) be   $\frac{y}{x}+sec(\frac{y}{x}),x>0.$  , then , the equation  of the curve is 

Answer:

Explanation:

Concept involved

 solving of homogeneous   differential equation  i.e,  substitute  $\frac{y}{x}=v$

 $\therefore$                        y=vx

     $\frac{dy}{dx}=v+x \frac{dv}{dx}$

  here, slope of the curve  at (x, y) is

   $\frac{dy}{dx}=\frac{y}{x}+sec(\frac{y}{x})$

 put      $\frac{y}{x}$=v

$\therefore$     $v+x \frac{dv}{dx}=v+sec(v)$

$\Rightarrow $      $ x \frac{dv}{dx}=\sec (v)$

$\Rightarrow$     $  \int_{}^{} \frac{dv}{\sec v}=\int_{}^{} \frac{dx}{x}$

 $\Rightarrow$     $  \int_{}^{} \cos v dv=\int_{}^{} \frac{dx}{x}$

$\Rightarrow $     $ \sin v=\log x+\log c$

$\Rightarrow$    $  \sin (\frac{y}{x})=\log (cx)$

 as it passes through  $(1,\frac{\pi}{6})$

  $\Rightarrow $    $ \sin(\frac{\pi}{6})=\log c$

  $\Rightarrow  \log c=\frac{1}{2}$

 $\therefore$        $\sin(\frac{y}{x})=\log x+\frac{1}{2}$

The area enclosed by the curves y= sin x+cos x and y=|cosx-sinx| over the interval  $\left[0,\frac{\pi}{2}\right]$ is

Answer:

Explanation:

Concept involved

 T o find the bounded area between y=f(x)  and y= g(x)  between  x=a to x= b

 $\therefore$ Area bounded

     $=\int_{a}^{c} [g(x) -f(x)]dx+\int_{c}^{b} [f(x)-g(x)]dx$

  $\Rightarrow \int_{a}^{b} |f(x)-g(x)| dx$

 Here , f(x)=y=sinx+cos x , when

              $0\leq x \leq\frac{\pi}{2}$

 and g(x) = y=|cos x-sinx |

   $=\begin{cases}\cos x- \sin x, & 0\leq  x\leq\frac{\pi}{4} \\\sin x-\cos x, & \frac{\pi}{4}\leq x \leq \frac{\pi}{2}\end{cases}$

Could  be shown as

$\therefore$ Area bounded

$=\int_{0}^{\frac{\pi}{4}} \left\{(sinx+cos x)-(cos x-sinx)\right\} dx$

              $+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \left\{(sinx+cos x)-(sin x-cosx)\right\} dx$

  $=\int_{0}^{\frac{\pi}{4}} 2 sin x dx+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} 2cos x dx$

  $=-2(cos x)^{\frac{\pi}{4}}_{0}+2(sin x.n)^{\frac{\pi}{2}}_{\frac{\pi}{4}}$

    $=4-2\sqrt{2}=2\sqrt{2}(\sqrt{2}-1)$

Four persons independently solve a certain problem  correctly with probabilities   $\frac{1}{2},\frac{3}{4},\frac{1}{4},\frac{1}{8}$ . Then, the probability that the problem is solved correctly by at least one of them is 

Answer:

Explanation:

 concept involved

 it is a simple application of independent event,  us to solve a certain problem or any type of competition each event is independent of order.

   Formula used 

 $P(A\cap B)=P(A).P(B)$    When A and B  are independent events

probability that the problem is solved correctly by atleast one of them =1-(problem is not solved by all)

$\therefore$  P (problem is solved )=1-P

(Problem is solved)

   $=1-P(\overline{A)}.P(\overline{B)}.P(\overline{C)}.P(\overline{D)}$

     = $1-\left(\frac{1}{2}.\frac{1}{4}.\frac{3}{4}.\frac{7}{8}\right)$

    =$1-\frac{21}{256}=\frac{235}{256}$

• Advanced 2013 - Physics 2013
• Advanced 2013 - Chemistry 2013
• Advanced 2013 - Mathematics 2013